Binary search, its use cases, and complexities

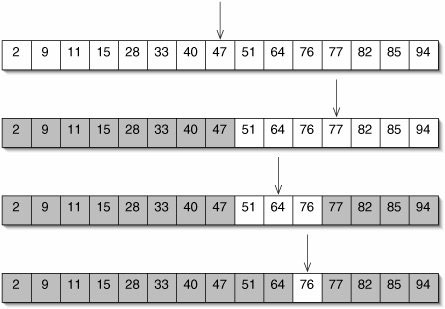
What is binary search?

A Binary search element approach; A binary search algorithm divides a search interval in half repeatedly in a sorted array.

Binary search utilizes the fact that the array is sorted to reduce the time complexity to O(log n). Understand all four simple steps by a professional software service provider that are involved in the binary search:

To begin, cover the whole array with an interval.

In case the key value is less than the item centered in the interval, narrow it to the lower half.

• To begin, cover the whole array with an interval.
• In case the key value is less than the item centered in the interval, narrow it to the lower half.
• If not, narrow it to the upper half.
• Continue checking until you find the value or the interval is empty.

You can implement binary search in two ways or there are 2 algorithm for binary search

• Iterative method
• Recursive method

Iterative Algorithm:

Iterative algorithms continuously repeat a specific set of statements. It recounts the same steps continuously; an iterative algorithm uses looping statements such as for loops, while loops, and do-while loops.

Algorithm:

do until the pointers low and high meet each other.
            mid = (low + high)/2
            if (x == a[mid])
              return mid
        else if (x > a[mid]) // x is on the right side
              low = mid + 1
        else                // x is on the left side
              high = mid - 1

Recursive Algorithm:

As a recursive algorithm, a function calls itself until it reaches the stopping condition (base condition).

Let us track the search space by using two indexes start and end. Initially low = 0 and high = n – 1(as initially, the whole array is search space). At each step, we find a mid-value in the search space and compare it with the target value. There are three cases possible:

Case 1: If the target is equal to the middle, then return mid.

Case 2: If the target is less than the middle i.e target<A[mid], we discard all the elements in the right search space including the mid element. Now our new high would be mid-1 while ‘low’ remains as it is.

Case 3: If the target element is greater than the middle i.e target>A[mid], we discard all the elements in the left search space including the mid element. Now our new low would be mid+1 while ‘high’ remains as it is.

Algorithm:

binarySearch(arr, x, low, high)
            if low > high
                return False 
            else
                mid = (low + high) / 2 
                if x == a[mid]
                    return mid
                else if x > a[mid] // x is on the right side
                    return binarySearch(arr, x, mid + 1, high)
                else               // x is on the right side
                    return binarySearch(arr, x, low, mid - 1)

1: Count the maximum number of positive and negative integers in an array

Assuming that the array a[] contains N integers, our task is to find the maximum among the counts of positive and negative integers in the array a[].

Example 1:

Input: a[] = {-19, -12, -7, -5, -1, 8, 12}

Output: 5

Explanation:

There are 2 positive numbers and 5 negative numbers. Among 5, 2 makes the maximum number: 5. Therefore, the output is 5.

Example 2:

Input: a[] = {-18, -11, 8, 14}

Output: 2

Explanation:

Here, the count of positive and negative numbers are the same which is why the output is 2.

Approach:

We can approach the given problem using Binary Search, the aim is to find the first index whose value is positive and print the maximum of both IDX and (N – IDX) as a result.

To solve the given problem, follow these steps:

• We can initially define two variables, low as 0 and high as (N – 1).
• Follow the below instructions to perform a Binary Search on the given array a[] by iterating until low <= high:
  • Calculate mid as (low + high) / 2.
  • If the value of mid is positive, then the right half shall be skipped by updating the high value to (mid – 1). Alternately, you may skip the left half by updating the value of low to (mid + 1).
• As a result, compute the maximum of low and (N – low).

Implementation of the above approach using Python:

def getMax(a, length):
            low = 0
            high = length - 1
            while (low <= high):
              mid = low + (high - low) # 2 - Find the value of mid
                  if (a[mid] < 0): # If element is negative then, ignore the left half
                     low = mid + 1
                  elif (a[mid] > 0): # If element is positive then, ignore the right half
                      high = mid - 1
                  return max(low, length - low) # Return maximum among the count of positive & negative element
        if __name__ == "__main__":
            a = [-19, -12, -7, -5, -1, 8, 12]
            n = len(a)
            print(getMax(a, n))

Output:

5

3

Time Complexity: O(log N)
Space Complexity: O(1)

2: Order-Agnostic Binary Search

Order-Agnostic Binary Search is an upgraded version of the Binary Search algorithm. It features an additional condition checking capability. The algorithm’s reasoning is based on what would happen if an array was sorted without a specified order. Here, you must ensure that the value of the first element is greater or smaller than the value of the last element.

Case 1: If the first element is larger than the last element, then if the search key value X is smaller than the middle of the interval, the end pointer will be changed to mid -1, or else the start

the pointer will be changed to mid + 1.

Case 2: When the first element is greater than the last element, the start pointer will move to the next element in the middle element, if X is less than the middle of the interval, otherwise the end

the pointer will move before the middle element.

Ultimately, if the value of the search key matches the middle element, then the element is found for the search.

Let us see the implementation of Order-Agnostic Binary Search with the help of an example.

Given an array, a[] of size N and an element X, and the array is sorted in any order(ascending or descending), the task is to find whether element X is present in the array or not. If yes, then print its index, else print -1.

Example 1:

Input: a[] = {43, 27, 10, 6, 1}, N=5, X=6

Output: 3

Explanation:

The array is sorted in descending order and the element is present at index 1.

Example 2:

Input: a[] = {1}, N=1, X=10

Output: -1

Approach:

The brute force approach is about finding all possible solutions to a particular problem. So, the brute force approach would be to linearly traverse the array and check for the element. Using binary search would improve this algorithm if the sort order of the array was known – ascending/descending. Alternatively, an order-agnostic binary search can be used as follows:
You can solve this problem by using Order-Agnostic Binary Search by following the steps below:

• As long as a[start] is less than a[end], initialize the boolean variable isAsc as true else as false.
• Using a while loop, traverse a curve until the start is less than the end and take the following steps:
  • As a starting point, initialize the variable middle as the average of start and end.
  • The value of middle should be returned as the answer if a[middle] equals X.
  • Assuming that the array is sorted ascendingly, perform the following steps:
    • The value of start is middle+1 if a[middle] is less than X, and the value of end is middle-1 otherwise.
  • Otherwise, if a[middle] is less than X, set the value of end as middle-1 or set the value of start as middle+1.
• If you perform the steps outlined above and no element is found, then return -1 as the answer.

Iterative implementation of Order-Agnostic Binary Search:

# Python program for the above approach using an iterative binary search.
        def binarySearch(a, start, end, x):
             isAsc = a[start] < a[end] # Checking the sorted order of the given array
             while (start <= end):
             middle = start + (end - start) // 2
             if (a[middle] == x): # Check if x is present at mid
            return middle
            if (isAsc == True): # Ascending order
            if (a[middle] < x): # If x greater, ignore left half
                 start = middle + 1
            else: # If x smaller, ignore right half
                 end = middle - 1
            else: # Descending order
            if (a[middle] > x): # If x smaller, ignore left half
                  start = middle + 1
              else: # If x greater, ignore right half
             end = middle - 1
               return -1 # Element is not present
        a = [ 60, 53, 35, 21, 17 ]
        x = 35
        n = len(a)
        print(binarySearch(a, 0, n - 1, x))

Output:

2

Time Complexity: O(log (N))
Space Complexity: O(1)

3: Identify the position of an element within an array of infinite numbers

When we see the array sorted, binary search immediately comes to mind, but there is a problem here since we don’t know how big the array is.

Due to the infinite nature of the array, there are no appropriate bounds to apply binary search. Therefore, to acquire the location of the key, we first determine the bounds and then run a binary search algorithm.

Example 1:

Input: a[] = {2, 5, 7, 9, 10, 12, 15, 16, 18, 20, 24, 28. 32, 35}, X = 16

Output: 7

Explanation:

The target is present at index ‘7’ in the array.

Example 2:

Input: a[] = {2, 5, 7, 9, 10, 12, 15, 16, 18, 20, 24, 28. 32, 35}, X = 19

Output: -1

Explanation:

The target is not present in the array.

Approach:

We can now compare the key with the high index element of the array by setting low to the 1st element and high to the 2nd element,

Case 1: When a key is greater than the high index element, duplicate the high index into the low index and double the high index.

Case 2: When smaller, apply a binary search between high and low indices found.

Implementation of the above approach using Python:

def binarySearch(a, left, right, x):
             if right >= left:
                  mid = left+(right-left)//2
                  if a[mid] == x:
                       return mid
                  if a[mid] > x:
                       return binarySearch(a, left, mid-1, x)
                  return binarySearch(a, mid+1, right, x)
        return -1
        
        def findPosition(a, key):
              left, right, val = 0, 1, a[0]
              while val < key:
                     left = right     #store previous high
                     right = 2*right  #double high index
                     val = a[right] #update new val
              return binarySearch(a, left, right, key)
        
        a = [3, 5, 7, 9, 10, 90, 100, 130, 140, 160, 170]
        ans = findPosition(a, 90)
        if ans == -1:
               print ("An element not found in list.")
        else:
               print("An element found at index ",ans)

Output:

An element found at index 5

Time Complexity: O(log P), where p is the position of the element to be searched.

Space Complexity: O(1)

4: Find the Kth smallest element in a 2D array that is sorted row-wise and column-wise

It pretty much takes care of itself when we speak of the Kth Smallest Element in a Sorted Matrix.

Therefore, we must find a number greater than or equal to exactly the K-1 elements of our matrix.

Matrixes can also be analyzed with Binary Search, but this is different from a conventional binary search because, instead of using the “index range”, we consider the “number range”(matrix values themselves). Generally speaking, we know that the smallest number in our matrix is at the top left corner and the biggest number is at the bottom lower corner. As a result, these two numbers can represent the Binary Search’s “range”, i.e., the values that are high and low.

Example:

matrix =

15, 25, 31, 43
16, 27, 36, 45
28, 30, 39, 49
33, 35, 40, 50

low=15 and high=50

Steps:

Iteration	low	high	mid	count	Explanation
1	15	50	32	7	count is not lesser than 3 => high = mid
2	15	32	23	2	count is lesser than 3 => low = mid + 1
3	24	32	28	5	count is not lesser than 3 => high = mid
4	24	28	26	3	count is not lesser than 3 => high = mid
5	24	26	25	3	count is not lesser than 3 => high = mid
6	24	25	24	2	count is lesser than 3 => low = mid + 1
7	25	25			low is not lesser than mid, the loop terminates

Approach:

• To begin the Binary Search, set low = matrix[0][0] and high = matrix[n-1][n-1].
• Calculate the midpoint of the low and the high. Note that this number is not necessarily part of the matrices.
• In the matrix, count all numbers smaller than or equal to mid. Since the matrix is sorted, this can be done in O(N).
• In the case where the count is less than ‘K’, we can set low = mid+1 to search the higher part of the matrix.
• Otherwise, if the count is equal to or greater than ‘K’, we can update high = mid to search in the lower part of the matrix in the next iteration.
• After a certain point, the low and high values become equal, and the loop ends. We narrowed down the search range to one matrix element iteratively by collecting the value of the Kth smallest element.

Implementation of the above approach using Python:

# This returns count of elements in matrix less than or equal to num
        def searchElementGreaterThanOrEqual(num, n, mat): 
             ans = 0
             for i in range(0,n):
                   # if num is less than the first element then no more element in matrix further are less than or equal to num
             if (mat[i][0] > num):
                 return ans
                  # if num is greater than last element, it is greater than all elements in that row
                if (mat[i][n - 1] <= num):
                    ans += n
                    continue
                   # This contain the col index of last element in matrix less than of equal to num
                 greaterThan = 0
                 jump = n//2
                 while (jump >= 1):
                     while (greaterThan + jump < n and mat[i][greaterThan + jump] <= num):
                          greaterThan += jump
                    jump = jump // 2
                 ans += greaterThan + 1
             return ans
        
        # returns kth smallest index in the matrix
             def kthSmallest(matrix, n, k):
                l = matrix[0][0]
                r = matrix[n-1][n-1]
                while (l <= r):
                 mid = l + (r - l) // 2
                       greaterThanOrEqualMid = searchElementGreaterThanOrEqual(mid, n, matrix)
                 if (greaterThanOrEqualMid >= k):
                   r = mid - 1;
                 else:
                    l = mid + 1;
                 return l;
        a =[[15,25,31,43],
           [16,27,36,45],
           [28,30,39,49], 
           [33,35,40,50]]
        print("3rd smallest element in matrix is " + str(kthSmallest(a, 4, 3)))

Output:

3rd smallest element in the matrix is 25

Time Complexity: O(N)
Space Complexity: O(1)

Conclusion

As a result of using the four approaches discussed in this post, I have solved a lot of coding problems and have been able to effectively use binary search with other data structures, like matrices and lists.

Additionally, to harness the Binary search, take help Bigscal. Here at Bigscal, we adept a team of skilled professionals. Our team can transform complex challenges into manageable solutions.

So, be daring at all times. It will pay off! Thanks for reading, and happy programming!

If you have any doubts or suggestions, feel free to commen

FAQ